Evaluating Limits Algebraically Pdf

| Posted on by

Limits

  1. Evaluating Limits Algebraically Worksheet Pdf
  2. Evaluating Limits Algebraically Kuta
  3. Evaluating Limits Algebraically Pdf Download

Evaluating Limits Algebraically Worksheet Pdf

Evaluating

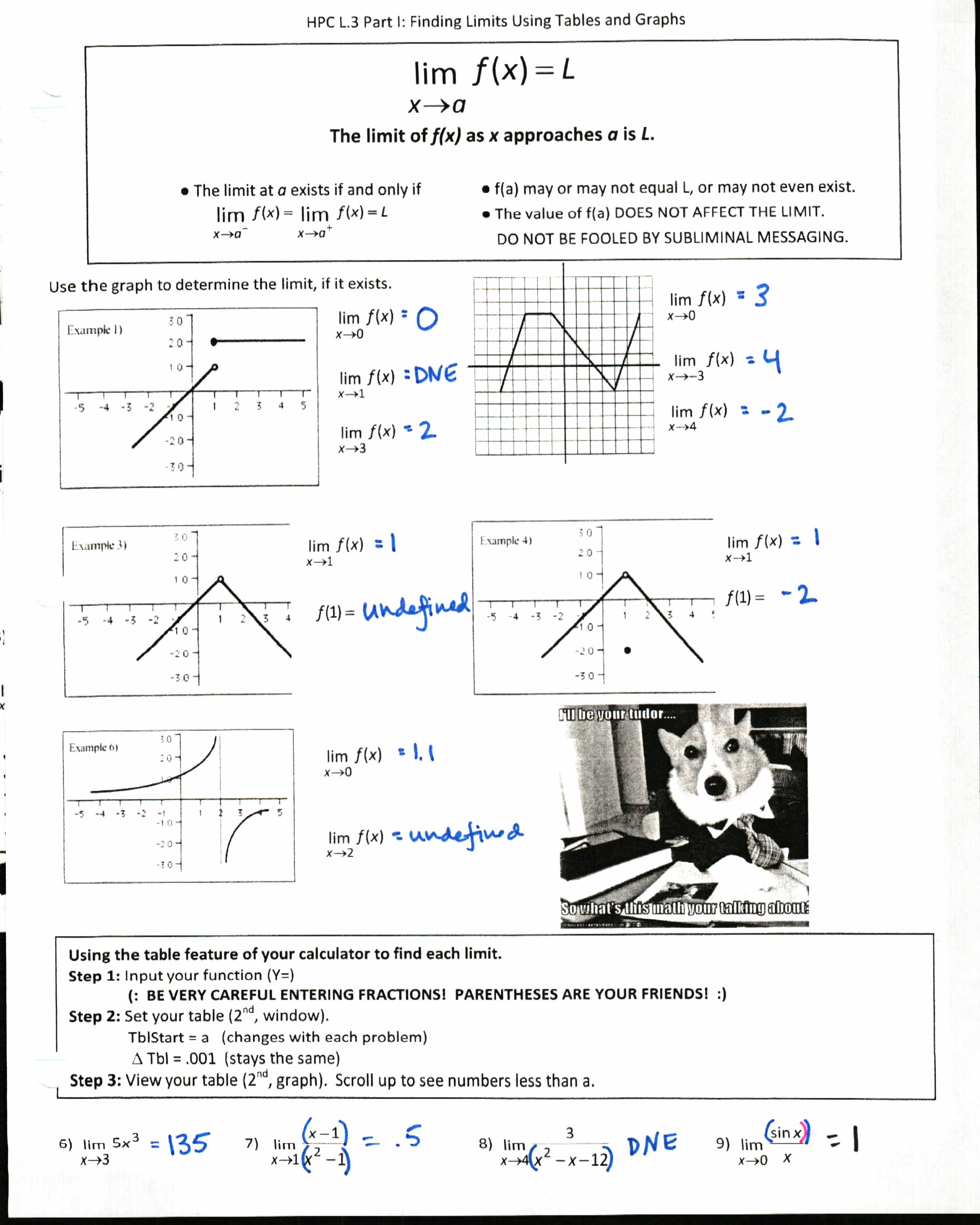
See if the one-sided limits are the same. If direct substitution gives 0 N where N ≠0, then the limit DNE (ex. E above) If direct substitution gives 0 N where N ≠0, then the limit = 0 4. If direct substitution gives 0 0 then try appropriate algebraic “tricks:” a. Factoring and reducing (ex a, e above) b. Evaluating*Limits*Worksheet* * Evaluate*the*following*limits*without*using*a*calculator.* 1) lim x→3 2x2−5x−3 x−3 2) lim x→2 x4−16 x−2 3) lim x→−1 x4+3x3−x2+x+4 x+1 4) lim x→0 x+4−2 x * * * * * * * * * 5) lim x→3 x+6−x x−3.

Show Mobile NoticeShow All NotesHide All Notes

Evaluating Limits Algebraically Kuta

You appear to be on a device with a 'narrow' screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 2-5 : Computing Limits

Evaluating limits algebraically pdf

For problems 1 – 9 evaluate the limit, if it exists.

  1. (mathop {lim }limits_{x to 2} left( {8 - 3x + 12{x^2}} right)) Solution
  2. (displaystyle mathop {lim }limits_{t to , - 3} frac{{6 + 4t}}{{{t^2} + 1}}) Solution
  3. (displaystyle mathop {lim }limits_{x to , - 5} frac{{{x^2} - 25}}{{{x^2} + 2x - 15}}) Solution
  4. (displaystyle mathop {lim }limits_{z to 8} frac{{2{z^2} - 17z + 8}}{{8 - z}}) Solution
  5. (displaystyle mathop {lim }limits_{y to 7} frac{{{y^2} - 4y - 21}}{{3{y^2} - 17y - 28}}) Solution
  6. (displaystyle mathop {lim }limits_{h to 0} frac{{{{left( {6 + h} right)}^2} - 36}}{h}) Solution
  7. (displaystyle mathop {lim }limits_{z to 4} frac{{sqrt z - 2}}{{z - 4}}) Solution
  8. (displaystyle mathop {lim }limits_{x to , - 3} frac{{sqrt {2x + 22} - 4}}{{x + 3}}) Solution
  9. (displaystyle mathop {lim }limits_{x to 0} frac{x}{{3 - sqrt {x + 9} }}) Solution
  10. Given the function [fleft( x right) = left{ {begin{array}{rc}{7 - 4x}&{x < 1}{{x^2} + 2}&{x ge 1}end{array}} right.]

    Evaluate the following limits, if they exist.

    1. (mathop {lim }limits_{x to , - 6} fleft( x right))
    2. (mathop {lim }limits_{x to 1} fleft( x right))
    Solution
  11. Given [hleft( z right) = left{ {begin{array}{rc}{6z}&{z le - 4}{1 - 9z}&{z > - 4}end{array}} right.]

    Evaluate the following limits, if they exist.

    1. (mathop {lim }limits_{z to 7} hleft( z right))
    2. (mathop {lim }limits_{z to - 4} hleft( z right))
    Solution

For problems 12 & 13 evaluate the limit, if it exists.

Evaluating Limits Algebraically Pdf Download

  1. (mathop {lim }limits_{x to 5} left( {10 + left| {x - 5} right|} right)) Solution
  2. (displaystyle mathop {lim }limits_{t to , - 1} frac{{t + 1}}{{left| {t + 1} right|}}) Solution
  3. Given that (7x le fleft( x right) le 3{x^2} + 2) for all x determine the value of (mathop {lim }limits_{x to 2} fleft( x right)). Solution
  4. Use the Squeeze Theorem to determine the value of (displaystyle mathop {lim }limits_{x to 0} {x^4}sin left( {frac{pi }{x}} right)). Solution